1. Introduction
As part of my bachelor’s thesis published in 2020 in information technology, I investigated a largely unknown weakness in a Bluetooth Low Energy (BT-LE) pairing process and developed a concept to prove it in practice. This concept could be tested with software that was also developed during the bachelor’s thesis.
The basis for this is a document[1] by Mr. Tomáš Rosa, who claims that a mathematical function for calculating confirmation parameters can be bypassed. He refers to the corresponding “Confirm value generation function”, which was first defined in the Bluetooth Core Specs. v.4.0 with BT-LE. It serves to ensure the authentication of both participants during the pairing of two BT devices. Unfortunately, the document is very compact and there is no comprehensive mathematical proof or practical evidence to support his thesis.
According to some research, this issue in particular has not been addressed by anyone since the publication of Rosa’s document in 2013. This is confirmed by all BT specifications that have been published since then, as the function and its parameters for calculating and checking confirmation parameters defined with the PassKey-Entry pairing method have remained unchanged. There is also no practical proof, tool or entry in the CVE database for this vulnerability. This gave rise to the idea of working through his findings and making them the subject of my thesis.
In the blog post, I present the results of my thesis in short form. In the end, the vulnerability was practically exploited and all tested devices of all BT-LE versions (v4.0-v5.1) are affected. As soon as a device supports the pairing method PassKey-Entry in the master role, the attack is possible.
2. Basics
2.1 PassKey-Entry Pairing
This is a pairing method for BT that establishes a authenticated connection between two BT-LE devices. The following picture shows the pairing sequence:
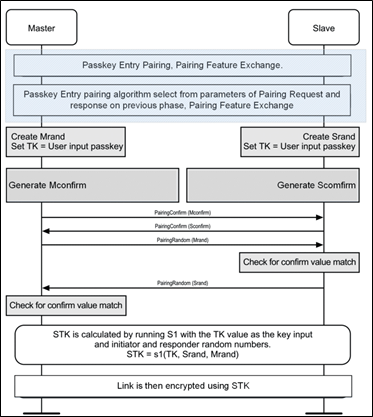
Pairing-Steps (After negotiation of the pairing method):
- Master and slave create a random value each (Master his Mrand; Slave his Srand).
- The master creates a TK (PIN e.g. ‘123456’) and presents it on his display.
- The slave must see the PIN to enter it on his device and set it as his TK (If so, both use the same TK for the following steps.).
- Both now create an independent confirm value under the usage of the following formula (3). (Master his Mconfirm; Slave his Sconfirm)
(1) ??????? = ?1(??,?,????,????,???,???,??,??)
(2) ?1 = ?????[?????( ? ⊕?1)⊕?2]
(3) (?|?)??????? = ?????[?????( (?|?)???? ⊕?1)⊕?2]
The parameters p1 and p2 are known on both sides after the initial “Pairing-Feature-Exchange”.
- As you can see in the flowchart, the parameters are exchanged as shown.
- Mconfirm form master to slave
- Sconfirm from slave to master
- Mrand from master to slave
- Now the slave can check whether it has the same PIN as the master. The slave checks it with formula (3) and compare it with the received Mconfirm.
(3) ???????? ?= ?????[?????(????? ⊕?1)⊕?2]
If the comparison is true, the pairing continues.
- The slave now sends his Srand to the master.
- Now the master can check whether it has the same PIN as the slave. The master check it with formula (3) and compare it with the received Sconfirm.
(3) S??????? ?= ?????[?????(S???? ⊕?1)⊕?2]
If the comparison is true, the pairing continues.
- Now the pairing and authentication between master and slave is finished.
2.2 The “Confirm-Value-Generation” Function
The “Confirm-Value-Generation” Function (c1, formula (2)) is used to calculate the M|Sconfirm parameters during the pairing process. The confirm-values are needed to check whether both sides have the same TK (PIN). Only if the slave sees the PIN on the master’s display, he can set the right TK on his device. With this, the authentication between master and slave is done. At first glance, it is not possible to change the equation so that we can calculate Srand. Why Srand? Let’s assume we (as an attacker) are the responder (the slave) of the pairing.
- To successfully bypass the authentication, we need TK. For the simple reason that we need the parameter to calculate the STK after the pairing for the following data encryption.
- We can’t calculate TK until we have received Mrand and Mconfirm.
- After we received Mconfirm we have to send Sconfirm. But we can’t calculate a valid Sconfirm without TK ☹.
- After we received Mrand, we can calculate the missing TK with formula (3). We brute-force any possible value for TK (‘000000’ – ‘999999’), until the equation gives a true statement. (Max. 106 calculations, ~<3s runtime with simple C code)
- Now we have the right TK, but we sacrificed a wrong Sconfirm to get the Mrand ☹.
- The only chance we have is to manipulate the Srand parameter to affect the confirm-value check on the master’s side. If it fails, the master will break the pairing.
This is where the vulnerability becomes important:
It’s possible to calculate Srand with the parameters Sconfirm (that we had to choose randomly) and TK (that we had brute-forced) so that the equation:
S??????? ?= ?????[?????(S???? ⊕?1)⊕?2]
gives a true statement on the master’s side.
3. Exploit
As mentioned in chapter 2.2, the “Confirm-Value-Generation” function can be misused to bypass the pairing authentication.
The problem is, that the equation can be changed to the parameter Srand so that the following applies:
????? = ?????−1[?????−1(????????)⊕?2]⊕?1
3.1 Procedure of the Attack
The following flowchart shows the attack process graphically.
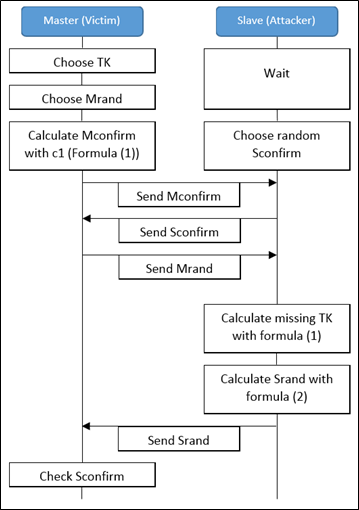
Please note:
Formula 1 is:
(1) S??????? = ?????[?????(S???? ⊕?1)⊕?2]
Formula 2 is:
(2) ????? = ?????−1[?????−1(????????)⊕?2]⊕?1
The exploit goes as follows:
- The attacker poses as an inconspicuous BT device (e.g., a BT speaker) and offers this inconspicuous service to the devices within range.
- It now waits until a victim wants to pair with the attacker’s device.
- The pairing runs as defined for the victim of the connection and he sends his calculated Mconfirm to the attacker.
- Next, the attacker can only send a random Sconfirm to the victim, but this does not harm the success of the pairing.
- Now the victim sends his random value Mrand to the attacker.
- The attacker can now calculate the PIN (TK), which is still unknown to him, by brute-forcing and using the formula (1) and the known parameters Mconfirm, Mrand, p1 and p2.
- The attacker can now calculate a value for Srand using the calculated TK and formula (2). For the parameter Sconfirm he uses his Sconfirm, which he chose randomly and sent to the victim in the fourth point.
- The attacker now sends the calculated Srand to his victim.
- The victim will now check whether the Sconfirm obtained in point four is valid. To do this, he calculates its own value for Sconfirm using the formula (1), the known parameters p1 and p2, and the value Srand just received from the attacker.
- If the formula (2) is correct, both values will be identical for Sconfirm and the victim will accept the value and continue the pairing.
It turns out that the formula (1) can be changed to formula (2) as suspected and thus the exploit is executable.
Using this procedure, authentication can be completely bypassed during PassKey-Entry pairing.
3.2 A software for Exploiting
As part of the practical proof, I developed a C program, which can be used to prove and test the vulnerability.
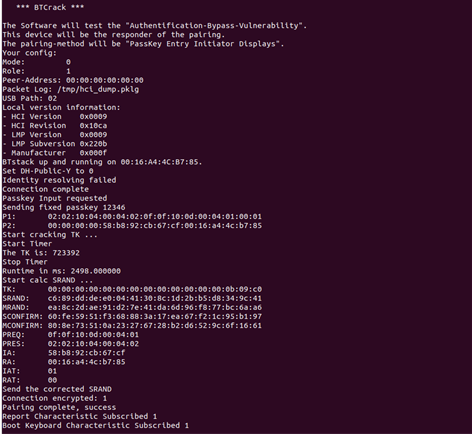
Now an attacker would have access to all BT-LE services that explicitly require authentication during pairing.
[1] Cryptology ePrint Archive von https://eprint.iacr.org/2013/309.pdf
- Bypass PassKey-Entry Authentication in BT-LE - 26. May 2021